量子计算对比特币的威胁：真的能破解吗？

作者：Max Moeller，CoinTelegraph；编译：白水，金色财经

一、量子计算与比特币的潜在威胁

比特币依赖于SHA-256哈希算法，这是由美国国家安全局（NSA）开发的一种加密算法。SHA-256在传统硬件上能够有效防止暴力破解攻击，因为利用现有技术解密可能需要数十年时间。然而，随着量子计算的兴起，这一安全屏障面临新的挑战。

量子计算基于量子物理原理，其核心是量子比特（qubit），可以同时存在于多种状态中。相比之下，传统计算机使用二进制比特（1和0）。1994年，数学家Peter Shor提出了一种算法，使量子计算机能够在几秒钟内解决传统硬件需要数十年才能完成的复杂算法。尽管当时尚无硬件能运行该算法，但近期Google Willow等技术的发展正逐步接近这一目标。

量子计算结合Shor算法可能会破坏比特币的加密系统。Shor算法的高效性使其能够快速解决复杂的数学问题，从而威胁到比特币的安全。

二、比特币面对的量子威胁：风险有多大？

比特币确实容易受到量子计算的影响，但具体风险如何？

创建加密钱包时，会生成两个关键部分：私钥和公钥。私钥是一段秘密代码，必须妥善保管；公钥由私钥生成，而钱包地址则由公钥生成。钱包地址用于接收加密货币，而私钥则是访问和管理资金的核心。

通过私钥生成公钥非常简单，但从公钥推导出私钥却极其困难——这几乎是不可能的，因此确保了钱包的安全性。每次发送加密货币时，私钥都会生成一个签名，证明您拥有资金并愿意发送。这一保护交易安全的系统被称为椭圆曲线数字签名算法（ECDSA）。

然而，量子计算被认为可能逆转这一过程，从公钥生成私钥。这种能力可能导致许多比特币持有者（尤其是早期用户和巨鲸）失去他们的资金。

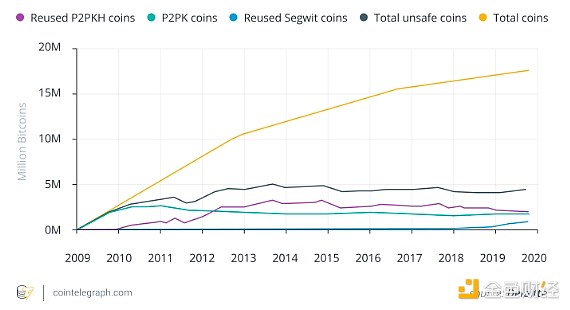
比特币地址类型及其量子风险

P2PK 地址类型

“支付到公钥”（P2PK）是2009年最常见的支付方式，主要用于比特币网络启动初期。这些地址较长（最多130个字符），不方便用户使用。

P2PK地址的钱包最容易受到Shor算法的攻击，因为它可以通过暴力破解推导出私钥。

P2PKH 地址类型

第二种地址类型是“支付到公钥哈希”（P2PKH），它比P2PK更抗量子攻击。P2PKH地址较短（33-34个字符），以“1”开头，并采用Base58编码。这些地址包含校验和以防止拼写错误。

P2PKH地址通过哈希处理公钥来提供更好的安全性。只有在您使用该地址进行支付时，公钥才会显示。如果从未发送过比特币，公钥将保持隐藏，从而提高抗量子攻击的能力。

然而，重复使用P2PKH地址会暴露公钥，增加漏洞。此外，当您从P2PKH地址支付时，公钥会在区块链上可见，从而使交易可追踪。

Taproot 地址

Taproot地址是2021年11月通过Taproot软分叉推出的最新地址类型。它使用Schnorr签名而非ECDSA签名，地址以“bc1p”开头，采用Bech32m编码，长度为62个字符。

Taproot地址提供了更强的隐私性。多重签名交易看起来像单签名交易，隐藏了复杂的支出条件。然而，Taproot地址会暴露公钥或经过调整的版本，使其容易受到Shor算法的攻击。

三、比特币的量子防御竞赛

虽然抗量子攻击是一项巨大挑战，但并非无法克服。

目前，量子计算机仍处于早期开发阶段，未来可能通过Shor算法推导私钥，从而破解比特币的加密技术。然而，这种威胁并非迫在眉睫，解决方案也已在研发中。

量子计算的发展不会孤立进行。相比去中心化的比特币区块链，政府和金融网络等中心化系统更容易成为攻击目标。这些系统使用过时的加密技术（如RSA），且存储敏感数据（如银行记录）。其单点故障使得入侵比攻击比特币的分布式节点更加容易。

国际货币基金组织警告称，量子计算机可能会颠覆移动银行业务。量子计算研究所的米歇尔·莫斯卡博士强调了“先收集后解密”的风险（攻击者今天存储加密数据，以便用未来的量子计算机解密）。2024年，七国集团网络专家组敦促金融机构评估量子风险，并指出中心化系统的数据可能因被拦截而暴露。

四、如何提升您的安全性以抵御量子威胁

尽管量子计算对比特币的威胁程度不如人们想象的那么高，但提前做好准备仍然至关重要。

• 避免重复使用公共地址：大多数加密钱包允许为每笔交易生成新地址，这有助于保护隐私。

• 将资金转移到私人钱包：如果您长期使用同一个公共地址，请考虑将资金转移到没有历史记录的新钱包。

• 使用不同的区块链网络：传统网络（如比特币和以太坊）的抗量子性能不如采用现代安全算法的新型网络。

• 保持信息灵通：及时了解量子计算的最新动态，以便采取相应措施。

虽然量子风险并非迫在眉睫，但开发人员和网络安全专家正在积极研究解决方案，以确保长期安全。与此同时，用户应及时关注比特币协议的更新和最佳实践，例如避免重复使用地址。